Decision Tree(결정 트리, 의사결정 트리, 의사결정 나무라고도 함)
기계학습(Machine Learning)에서 알고리즘으로 분류(Classification) 또는 회귀(Regression) 분석 목적으로 사용 → 지도학습(supervised learning)으로 종속변수의 기존 데이터를 분석하여 신규 데이터를 예측한다.
분류와 회귀에 사용될 수 있는데 먼저 분류를 알아보자
분류 → 정수
회귀 → 실수
목표 변수 유형에 따른 의사결정 트리
1) 범주형 목표 변수 : 분류 트리(Classification Tree- 카이 제곱, 지니지수, 엔트로피 사용)
목표 변수가 이산형(정수 ex) 0,1)인 경우, 각각의 범주(ex 사망, 생존)에 속하는 빈도에 기초해 분리 발생 → 분류 트리 구성
→ 계수를 가지고 분류 → 분류는 무조건 결과가 정수
2) 연속형 목표 변수 : 회귀 트리(Regression Tree)
목표 변수가 연속형(실수 ex) 2022년 12월 31일 주식 종가→ 22801.0)인 경우, 평균과 표준편차에 기초해 분리 발생 → 회귀 트리 구성
→ 회귀는 무조건 결과가 실수
Decision Tree의 구성
1) 마디(node) - 나무에서 분할되는 부분들
뿌리 마디(root node), 부모 마디, 자식 마디, 끝마디(terminal node)
가지, 깊이로 구성됨
2) 부모 마디(노드)로부터 자식 마디(노드)들이 형성될 때, 생성된 자식 노드에 속하는 자료의 순수도(Purity)가 가장 크게 증가하도록 트리를 형성하며 진행
입력 변수를 이용해 목표 변수의 분포를 얼마나 잘 구별하는 정도를 파악해 자식 마디가 형성되는데, 목표 변수의 구별 정도를 불순도(Impurity, 다양한 범주들의 개체들이 포함되어 있는 정도)에 의해 측정
불순도를 수치화 → Entropy, Gini Index
1) 엔트로피(Entropy)로 계산한 알고리즘 → ID3
2) 지니계수(Gini Index)로 계산한 알고리즘 → CART
Entropy - 불순도를 측정하는 지표 → 정보량의 기댓값
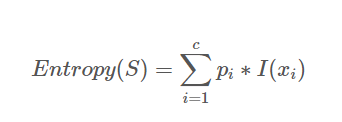
S : 이미 발생한 사건의 모음
c : 사건의 개수
정보량
어떤 사건이 가지고 있는 정보의 양
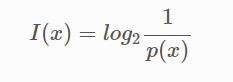
p(x) 사건 x가 발생할 확률
사건 x가 발생할 확률이 증가할수록 정보량은 0에 수렴 → 자주 발생하는 사건일수록 그다지 많은 정보를 가지고 있지 않다.
순도 100% → Entropy = 0
불순한 상태일수록 Entropy가 큰 값을 가지며 분류하기 어렵다.
ID3 알고리즘 (독립변수가 범주형)
엔트로피로 불순도를 계산하며, 독립변수가 모두 범주형 일 때만 사용 가능
→ 독립변수가 연속형일 때 사용하는 C4, C5도 존재해요!
정보획득량 - 분할전 Entropy와 분할 후 Entropy의 차이
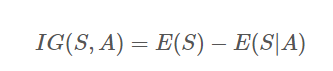
A : 속성(Feature)
E : Entropy(불순도)
정보획득량이 크다 → 어떤한 속성으로 분할했을 때 불순도가 줄어든다.
가지고 있는 모든 속성(Feature)에 대해 분할 후 정보획득량을 계산하고
그 값중 가장 큰 속성으로 분할의 기준을 삼아야 해요.
지니계수(Gini Index)
불순도를 측정하는 지표로서, 데이터의 통계적 분산 정도를 정량화해서 표현한 값(0~1 사이의 값)
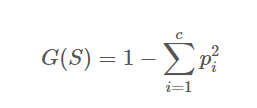
S : 이미 발생한 사건의 모음
c : 사건의 개수
지니계수(Gini Index)가 높을수록 데이터가 분산됨, 순수한 데이터 집합 =0
즉, 지니 지수가 작을수록 잘 분류된 것으로 볼 수 있음
CART 알고리즘
불순도를 지니계수(Gini Index)로 계산한다.
CART 알고리즘은 ID3 알고리즘과 달리 Binary Split 형태를 따른다
타깃과 그 외의 경우를 각각 계산하여 2개의 가지만 뻗는다.
독립변수가 연속형 일 때 Split
1) 전체 데이터를 모두 기준점으로 분할 후 불순도 계산
2) 중위수, 사분위수를 기준점으로
3) Label의 Class가 바뀌는 수를 기준점으로
앙상블(Random Forest) → Decision Tree의 과적합 해결 방법(가지치기)
tree의 모든 terminal node를 순도 100%로 만들면(Full Tree 상태) 분기가 너무 많아 과적합 발생!
가지치기(Pruning)
의사결정 나무에서 과적함을 방지하기 위해 적절한 수준에서 terminal node를 결합해 주는 것
가지치기의 종류
1) 사전 가지치기 → 트리의 최대 depth, 각 노드에 있어야 할 최소 관측 값 수 등을 미리 지정하여
트리를 만드는 도중에 stop 하는 것
* scikit-learn은 사전 가지치기만 지원
2) 사후 가지치기 → 트리를 먼저 Full tree로 만든 후 적절한 수준에서 terminal node를 결합해 주는 것
Cost-Complexity
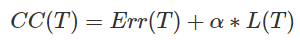
CC(T) : Tree의 비용 복잡도
Err(T) : 오분류율(불순도)
L(T) : terminal node의 수 = 구조 복잡도
Alpha(CP) : Err(T)와 L(T)를 결합하는 가중치 → CP(Complexity parameter)
CP(Complexity parameter) → 트리의 복잡도를 조정
Alpha가 커지면 tree의 terminal node가 조금만 많아도 CC 값이 확 커지기 때문에 가지를 쳐내 단순한 모델로 만듦
Alpha가 작아지면 terminal node가 많아도 CC 값이 커지지 않기 때문에 조금 더 복잡한 모델 생성
앙상블 - 여러 개의 Model을 조합하여 과적합을 방지하고, 예측의 정확도를 높이는 방법
과적합을 방지하는 방법 중 하나로, 대표적으로 Random Forest, gradient boosting 등이 있다.
랜덤 포레스트(Random Forest)
훈련을 통해 구성해놓은 다수의 나무들로부터 분류 결과를 취합해서 결론을 얻는, 일종의 투표(과반수 투표)
몇몇의 tree가 과적합을 보여도 다수의 tree를 기반으로 예측하기 때문에 그 영향력이 감소하게 되어 좋은 일반화 성능을 보임
배깅(Bagging)
각 분할에서 전체 속성들 중 임의로 일부만 고려하여 트리를 작성 하나의 분류기 역할(* 중복 허용)
ex) 총 50개의 나무 중 5개씩 선택
1) Bagging Features
트리를 만들 때 사용될 속성(feature)들을 제한함으로써 각 나무들에 다양성 부여
경험적으로 전체 속성 개수의 제곱근만큼 선택하는 게 가장 좋다고 함
2) Bagging parameter
n_estimators
-결정 트리의 개수를 정한다. 디폴트는 10개이며 많을수록 시간이 오래 걸린다는 단점이 있다.
max_features
-전체 피처 개수만큼 고려하여 분류한다. 분류할 때 기준이 있어야 하는데 그때 기준이 됨.
max_depth
-과적합을 개선하기 위해 사용되는 파라미터
'머신러닝 딥러닝' 카테고리의 다른 글
| 0118 confusion matrix( 오차 행렬), Information Gain(IG) (0) | 2022.01.18 |
|---|---|
| 0117 Random Forest (0) | 2022.01.17 |
| 1004 CNN 구조 정리, Fine Tuning (0) | 2021.10.04 |
| 1001 Data Augmentation (0) | 2021.10.01 |
| 0930 Image generator (0) | 2021.09.30 |



댓글