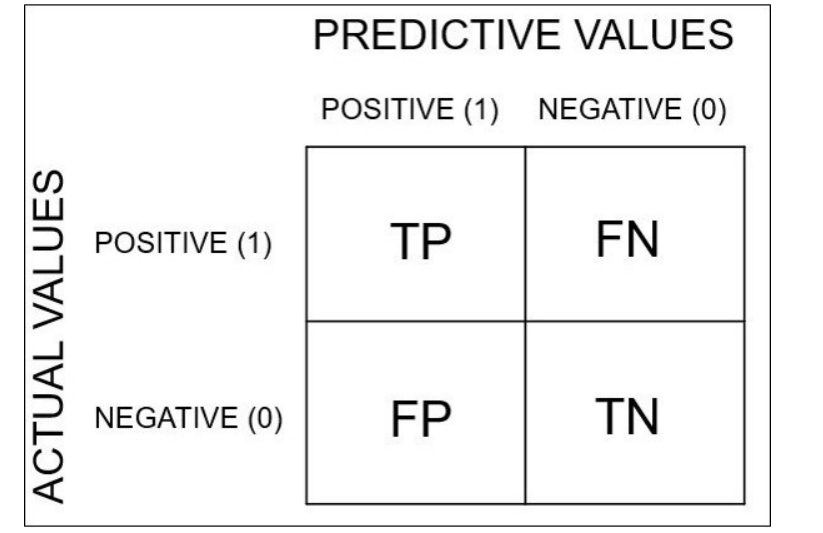
confusion matrix( 오차 행렬)
우리가 만든 logistic regression이 잘 만들어진 model 인지를 평가하는 지표.(로지스틱의 특징은 0,1로 나와요)
→ 우리의 model이 예측한 결과와 실제 정답(Lable)의 차이를 이용해서 모델의 정확도를 계산할 수 있어요!
1. Accuracy
전체 중 모델이 바르게 분류한 비율 → confusion matrix의 대각선
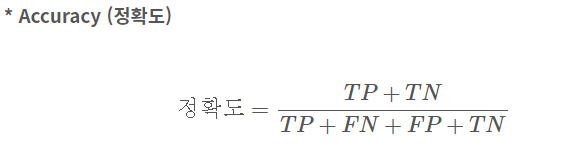
일반적으로 정확도로 많이 사용(직관적)
하지만 Domain(내가 가지고 있는 Data의 bias(편차)에 상당히 민감해요.
→ 데이터가 한쪽으로 치우쳐져 있는 경우
2.Precision(정밀도) 정확도랑 착각 Nono~
모델이 Positive라 분류한 것 중 실제 Positive인 비율 → confusion matrix의 첫 번째 열 방향

→ Recall(재현도)와 반비례, 1에 가까워질수록 정밀도가 높아요.
3. Recall(재현도, Hit rate, sensitivity)
실제 값이 Positive인 것 중 모델이 Positive라 분류한 비율 → confusion matrix의 첫 번째 행 방향
1로 가까워질수록 재현도가 높아요 → precision 과 반비례

4. F1 Score(F-Measure)
precision과 recall의 조화평균
→ confusion matrix의 첫 번째 행, 열

데이터가 한쪽으로 편향될 때 쓰면 좋다.
다중 Class에서 F1 Score 구하는 법 - 각 Class에 대한 Precision을 구한 후,
평균값으로 F1 Score 계산
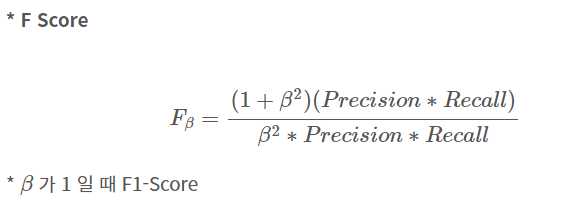
5. Fall-out
실제 False인 data 중에서 모델이 True라고 예측한 비율
→ 즉, 모델이 실제 false data인데 True라고 잘못 예측(분류) 한 것
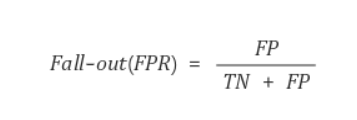
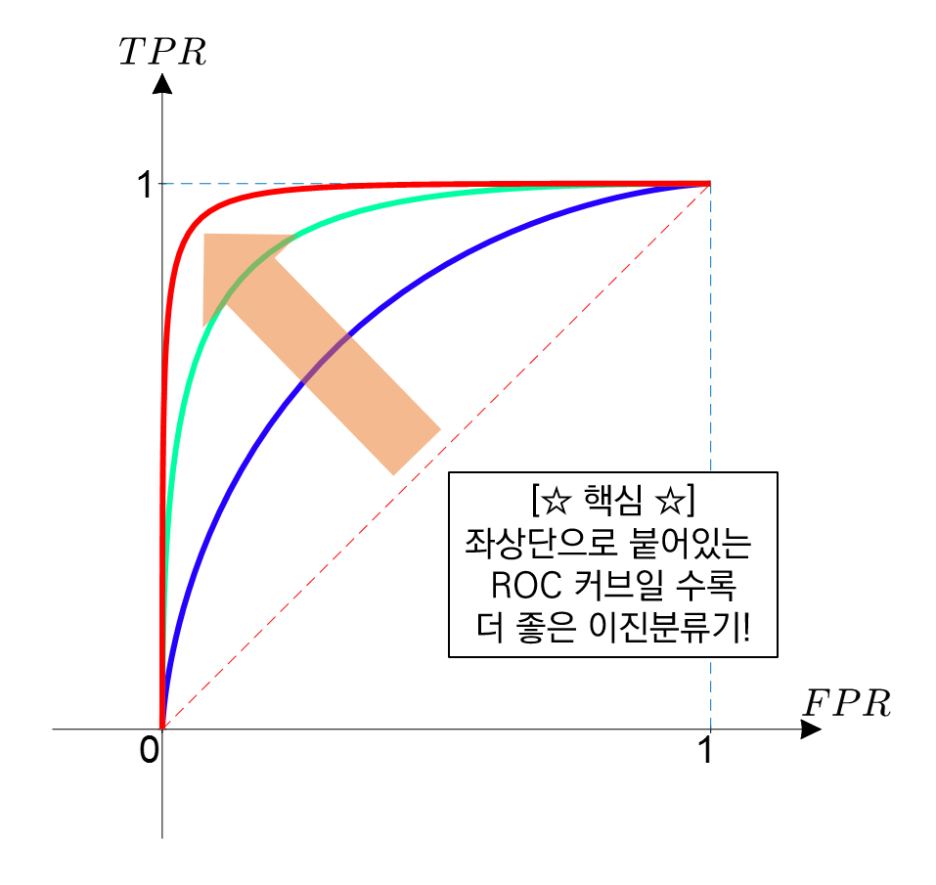
6. ROC curve
Recall과 Fall-out의 변화를 시각화한 그래프
Fallout은 실제 False인 data 중에서 모델이 True로 분류한, 그리고 Recall은 실제 True인 data 중에서 모델이 True로 분류한 비율을 나타낸 지표
이 두 지표를 각각 x, y의 축으로 놓고 그려지는 그래프를 해석
→ curve가 왼쪽 위 모서리에 가까울수록 모델의 성능이 좋다고 평가합니다. 즉, Recall이 크고 Fall-out이 작은 모형이 좋은 모형인 것입니다. 또한 y=x 그래프보다 상단에 위치해야 어느 정도 성능이 있다고 말할 수 있습니다.
classification_report 보는 법
support - 분류된 수
accuracy부터 밑에 있는 support - 전체 데이터 수
macro avg - 단순평균
weight avg - 가중 평균
분류된 개수/전체 데이터 수
ex) precision의 가중평균
(0의 계산된 precision * support + 1의 계산된 precision * support) / 전체 데이터 수
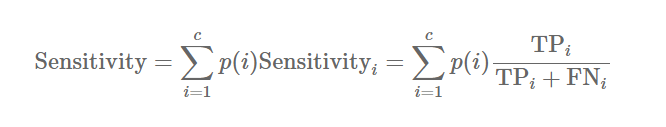
Entropy
정보량을 의미
|
엔트로피(Entropy)
|
정보량
|
확률
|
|
높다
|
많다
|
낮다
|
|
낮다
|
적다
|
높다
|
ex) 해가 동쪽에서 뜬다(100% 확률) → 엔트로피 낮다, 정보량이 적다.
해가 서쪽에서 뜬다(0% 확률) → 엔트로피 높다, 정보량 많다.
Information Gain(IG)
어떤 속성을 선택함으로 인해서 데이터를 더 잘 구분하게 되는 것
Information Gain을 계산해서 컬럼 중요도 계산(0~1 사잇값 가짐)
원래 Gini가 높았는데(막 섞여있음) 이 컬럼 값으로 분류하니까 Gini가 낮아짐(잘 분류) 일 때
Information Gain 값이 높아요(변별력이 좋다.)
어떤 분류를 통해 얼마나 Information(정보)에 대한 gain(이득)이 생겼는지를 나타낸다.
→ Entropy 사용(상위 노드의 엔트로피 - 하위 노드의 엔트로피)
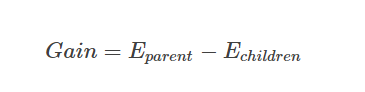
어떠한 특징(속성)을 선택함으로써 example을 구분하게 될 때 감소되는 entropy의 양 → 데이터를 잘 구분
Information Gain에서 모든 사건이 평균적인 확률을 지닐 때 가장 엔트로피가 높게 나타냄
자식들의 지니가 0일 때 Information Gain이 크고 자식들의 지니가 클 때 Information Gain이 낮다.
Information Gain 크다 → 순도(Purity)가 더 높게 나뉘었다.(더 잘 분류되도록 나뉘었다)
Information Gain이 없을 때(부모 노드의 정보량과 자식노드의 정보량의 차이가 없을때)
→ Tree는 분기(split)을 멈춤(정보 획득이 없기 때문)
칼럼의 중요도
값이 큰게 좋아요(Information Gain가 큰 칼럼 → 원래 Gini가 높았는데 분류하고 나서 Gini가 낮아진 칼럼)
[Applied Predictive Modeling] Feature Importances 특성 중요도
study 우선순위 렉쳐노트에서 특성 중요도 구하는 방법 3가지와 xgb 학습 과정 전반적으로 이해하기. 과제 제출 내데이터 조합하기 그걸로 과제.. xgboost 개념 이해하기 Feature Importances 질문 정리 특
mindsee-ai.tistory.com
여담으로 보통의 경우 엔트로피(Entropy)가 지니보다 더 높은 성능을 낸다.(평가에 더 가혹하다)
반면 연산 속도는 지니가 엔트로피를 더 앞선다.(로그를 사용하기 때문)
→ 시간을 투자해서라도 조금 더 나은 성능을 얻고자 할 때 Entropy,
준수한 성능과 빠른 계산을 원할 때 Gini 사용
지니(Gini) vs 엔트로피(Entropy) 그리고 정보 이득량(Information Gain)
안녕하세요, 끙정입니다. 오늘은 Tree Based Method에서 파티션(노드)을 분할할 때 기준으로 쓰이는 두 가지 측정방법, Gini(지니)와 Entropy(엔트로피)를 알아보겠습니다. 그리고 추가로 Information Gain(정
wyatt37.tistory.com
'머신러닝 딥러닝' 카테고리의 다른 글
| 0119 Ensenble, XGBoost (0) | 2022.01.19 |
|---|---|
| GridSearchCV (0) | 2022.01.19 |
| 0117 Random Forest (0) | 2022.01.17 |
| 0114 Decision Tree (0) | 2022.01.14 |
| 1004 CNN 구조 정리, Fine Tuning (0) | 2021.10.04 |



댓글